5 Variasi Soal tentang Segitiga Siku-Siku dan Cara Penyelesaiannya

rumus luas segitiga (dok. pribadi/Milla)

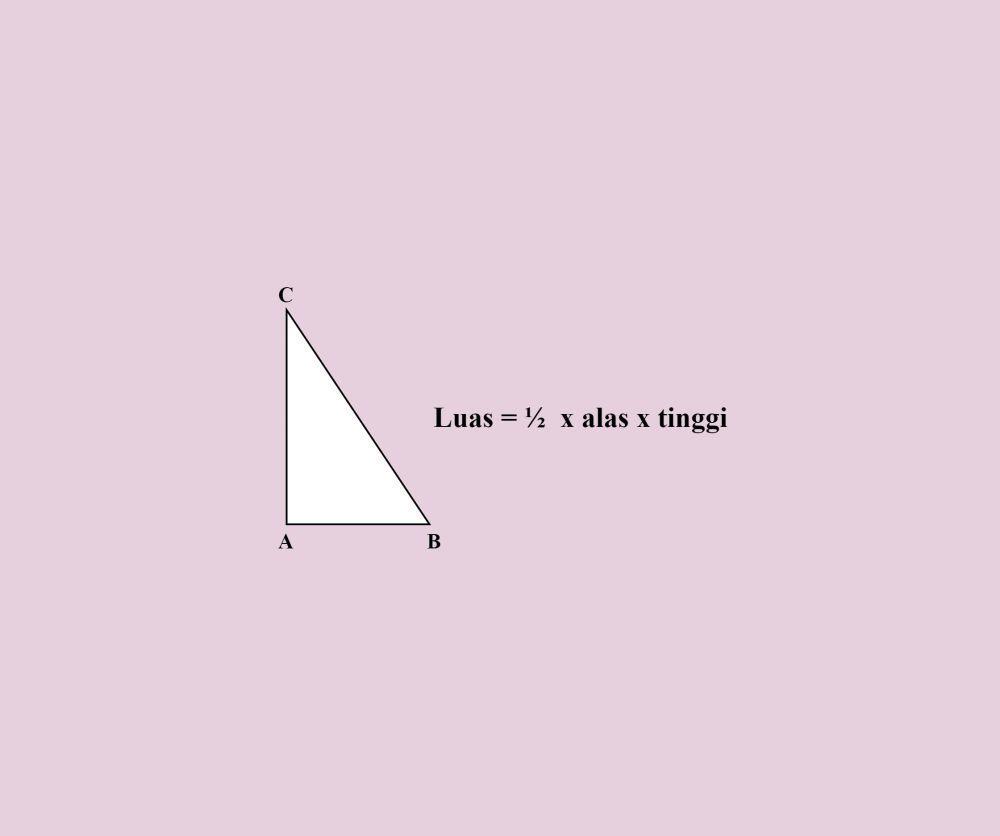
Sedangkan untuk menghitung keliling segitiga siku-siku kita dapat menggunakan rumus berikut.

rumus keliling segitiga (dok. pribadi/Milla)

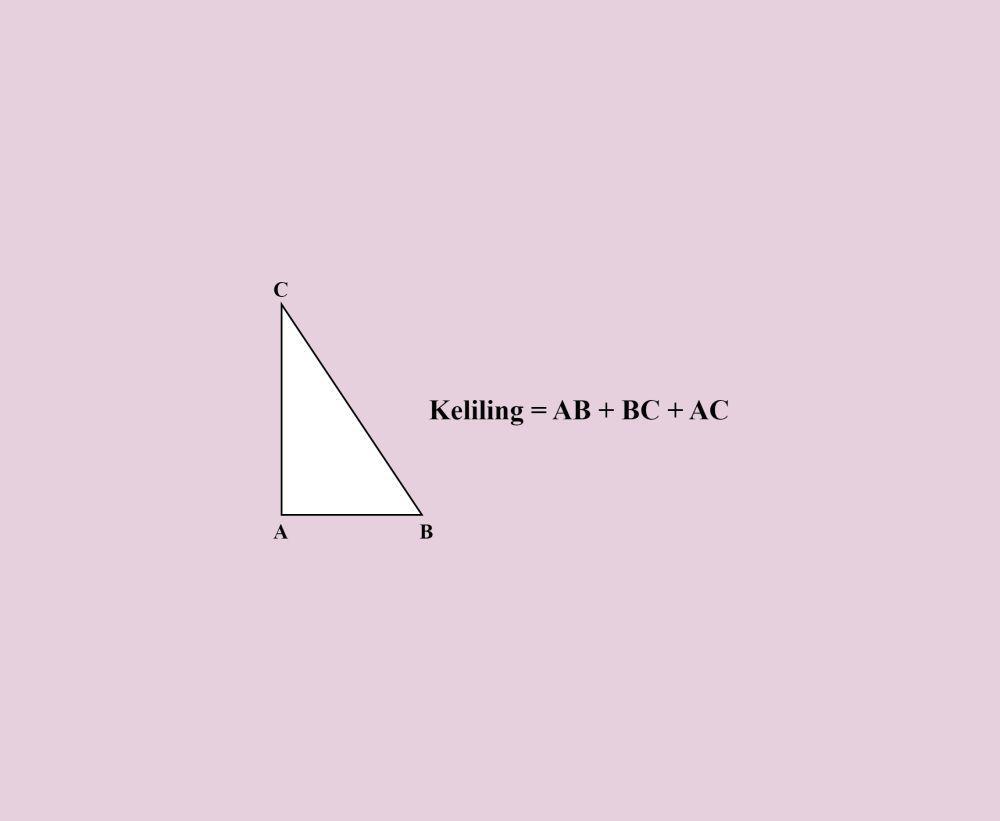
Selain rumus luas dan keliling, rumus Pythagoras juga perlu diketahui dan dipahami. Rumus Pythagoras akan sangat berguna untuk membantu kita menemukan panjang sisi dari segitiga siku-siku yang belum diketahui. Berikut adalah rumus Pythagoras.

rumus pythagoras (dok. pribadi/Milla)

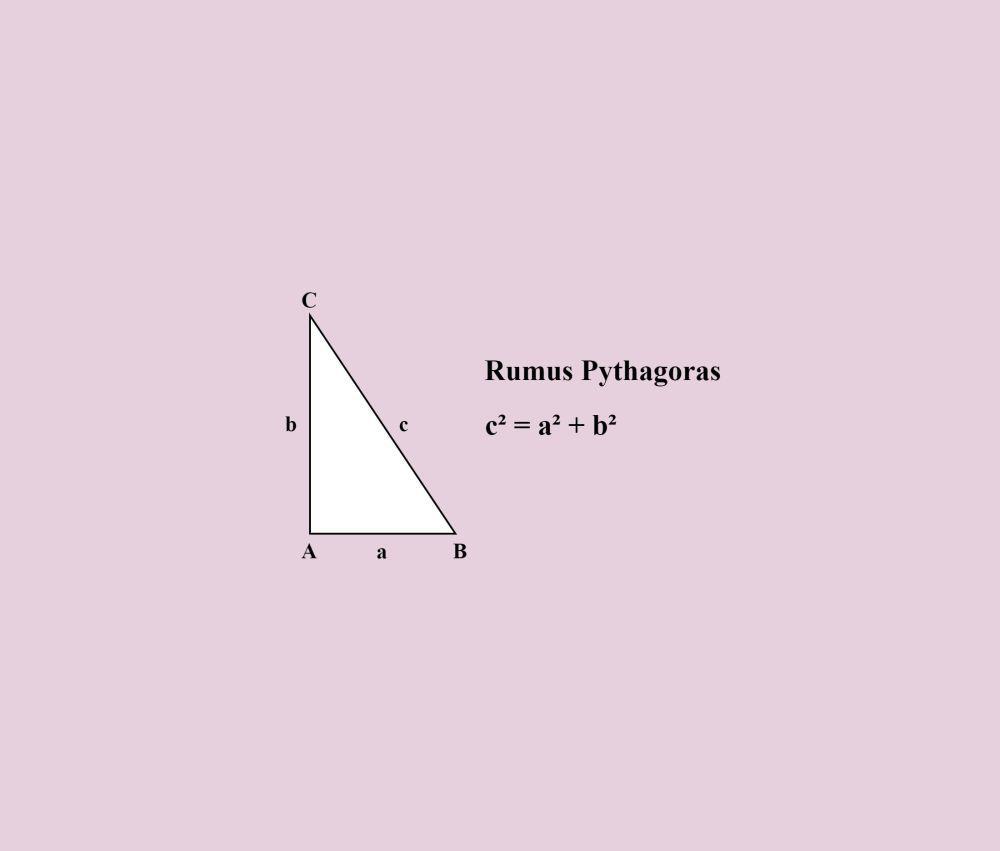
Sekarang mari terapkan rumus-rumus di atas untuk mengerjakan soal-soal di bawah ini.

soal 1 menghitung luas dan keliling segitiga siku-siku (dok. pribadi/Milla)

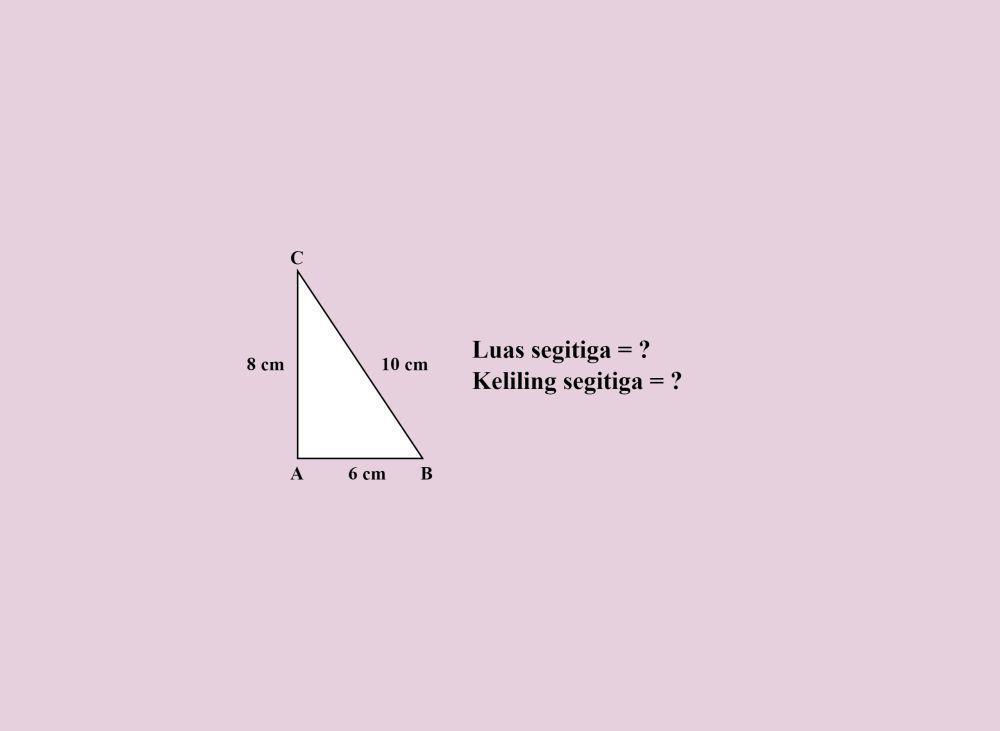
Hitunglah luas dan keliling segitiga siku-siku di atas!

Pembahasan:
Diketahui:
AB = 6 cm
BC = 10 cm
AC = 8 cm
Ditanya:
Luas segitiga = ?
Keliling segitiga = ?
Jawaban:
Luas segitiga = ½ x alas x tinggi
Luas segitiga = ½ x 6 x 8
Luas segitiga = ½ x 48
Luas segitiga = 24 cm²
Jadi luas segitiga ABC adalah 24 cm².

Keliling segitiga = AB + BC + AC
Keliling segitiga = 6 + 10 + 8
Keliling segitiga = 24 cm
Jadi keliling segitiga adalah 24 cm.

soal 2 mencari panjang sisi segitiga siku-siku (dok. pribadi/Milla)

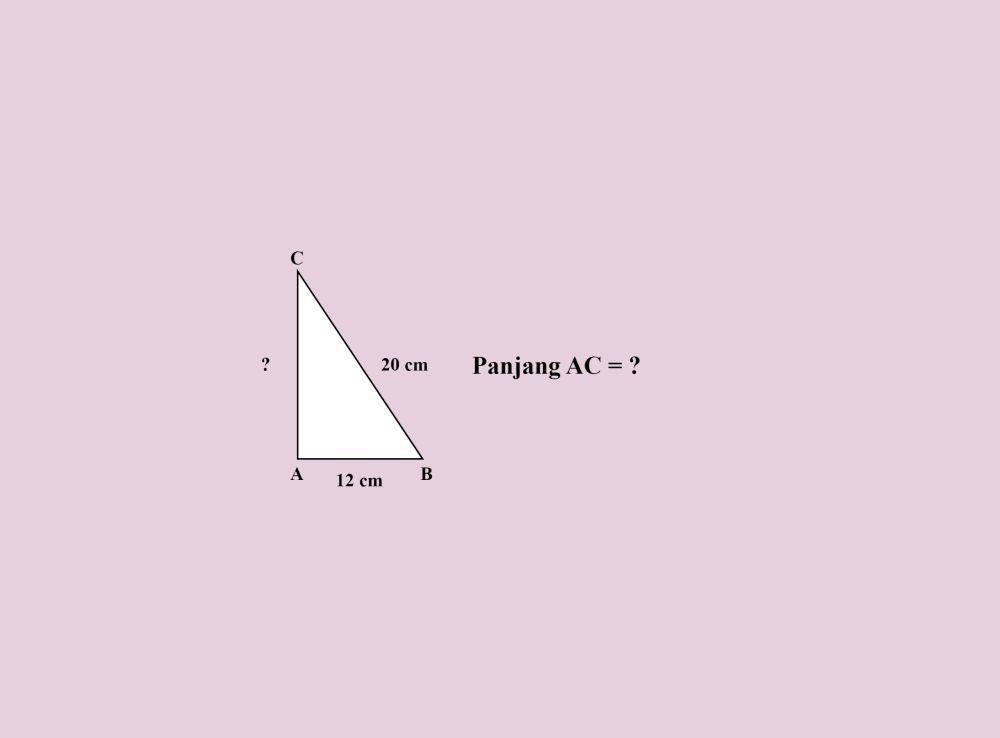
Jika panjang AB adalah 12 cm dan panjang BC adalah 20 cm, berapakah panjang AC?

Pembahasan:
Diketahui:
AB = 12 cm
BC = 20 cm
Ditanya:
AC = ?
Jawaban:
Untuk mencari panjang AC yang merupakan tinggi dari segitiga siku-siku kita dapat menggunakan rumus Pythagoras.
c² = a² + b²
BC² = AB² + AC²
AC² = BC² - AB²
AC² = 20² - 12²
AC² = 400 - 144
AC² = 256
AC = 16
Jadi panjang AC adalah 16 cm.

soal 3 menghitung luas segitiga siku-siku (dok. pribadi/Milla)

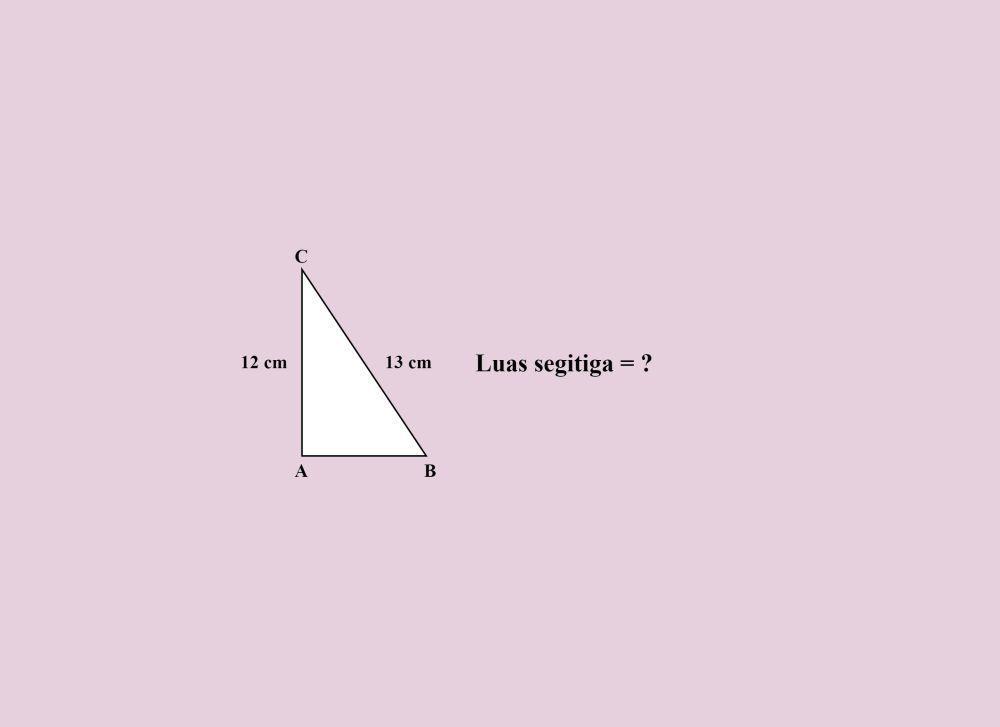
Sebuah segitiga ABC memiliki panjang BC = 13 cm dan panjang AC = 12 cm. Hitunglah luas segitiga ABC!

Pembahasan:
Diketahui:
BC = hipotenusa (sisi miring) = 13 cm
AC = tinggi segitiga = 12 cm
Ditanya:
Luas segitiga ABC = ?
Jawaban:
Untuk dapat menghitung luas segitiga tersebut, kita perlu mencari panjang AB dengan menggunakan rumus Pythagoras terlebih dahulu.
c² = a² + b²
BC² = AB² + AC²
AB² = BC² - AC²
AB² = 13² - 12²
AB² = 169 - 144
AB² = 25
AB = 5
Jadi panjang AB adalah 5 cm.

Luas segitiga = ½ x alas x tinggi
Luas segitiga = ½ x 5 x 12
Luas segitiga = ½ x 60
Luas segitiga = 30 cm²
Jadi luas segitiga ABC adalah 30 cm².

soal 4 menghitung keliling segitiga siku-siku (dok. pribadi/Milla)

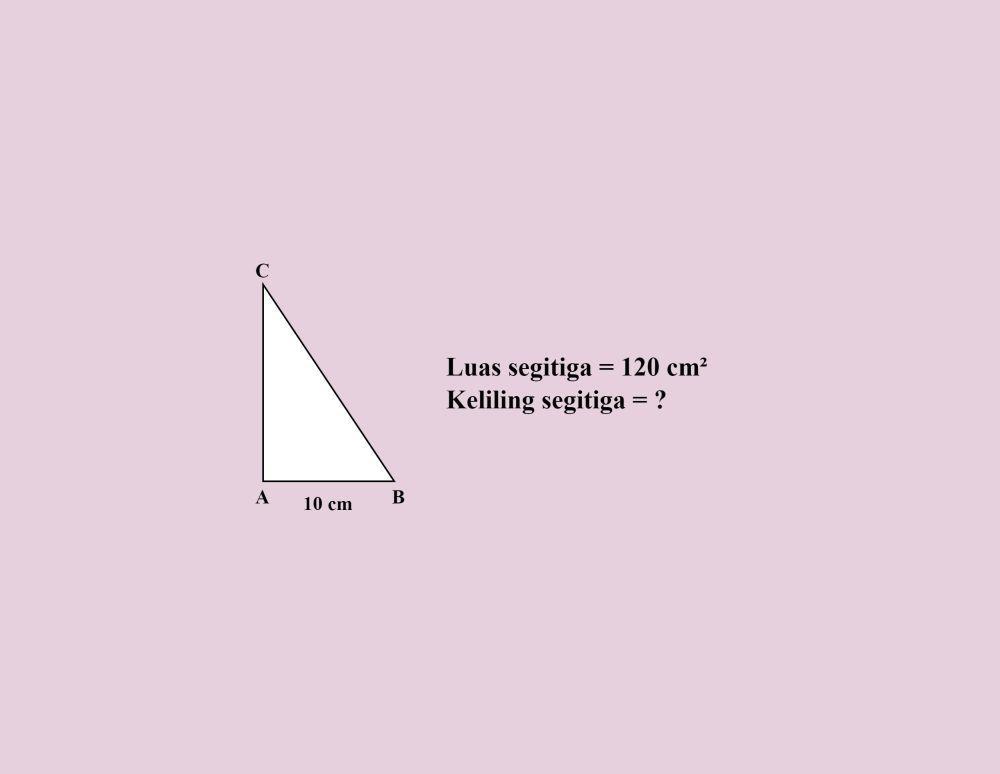
Diketahui luas segitiga ABC = 120 cm² dan panjang AB = 10 cm. Hitunglah keliling segitiga ABC!

Pembahasan:
Diketahui:
Luas segitiga = 120 cm²
AB = 10 cm
Ditanya:
Keliling segitiga = ?
Jawaban:
Untuk menghitung keliling segitiga tersebut, kita harus mencari panjang AC (tinggi segitiga) dan BC (sisi miring) dengan memanfaatkan informasi yang sudah disediakan dalam soal.
Luas segitiga = 120
½ x alas x tinggi = 120
½ x 10 x AC = 120
5 x AC = 120
AC = 24 cm
Jadi panjang AC adalah 24 cm.

c² = a² + b²
BC² = AB² + AC²
BC² = 10² + 24²
BC² = 100 + 576
BC² = 676
BC = 26 cm
Jadi panjang BC adalah 26 cm.

Keliling segitiga = AB + BC + AC
Keliling segitiga = 10 + 26 + 24
Keliling segitiga = 60 cm
Jadi keliling segitiga ABC adalah 60 cm.

soal 5 mencari besar sudut segitiga siku-siku (dok. pribadi/Milla)

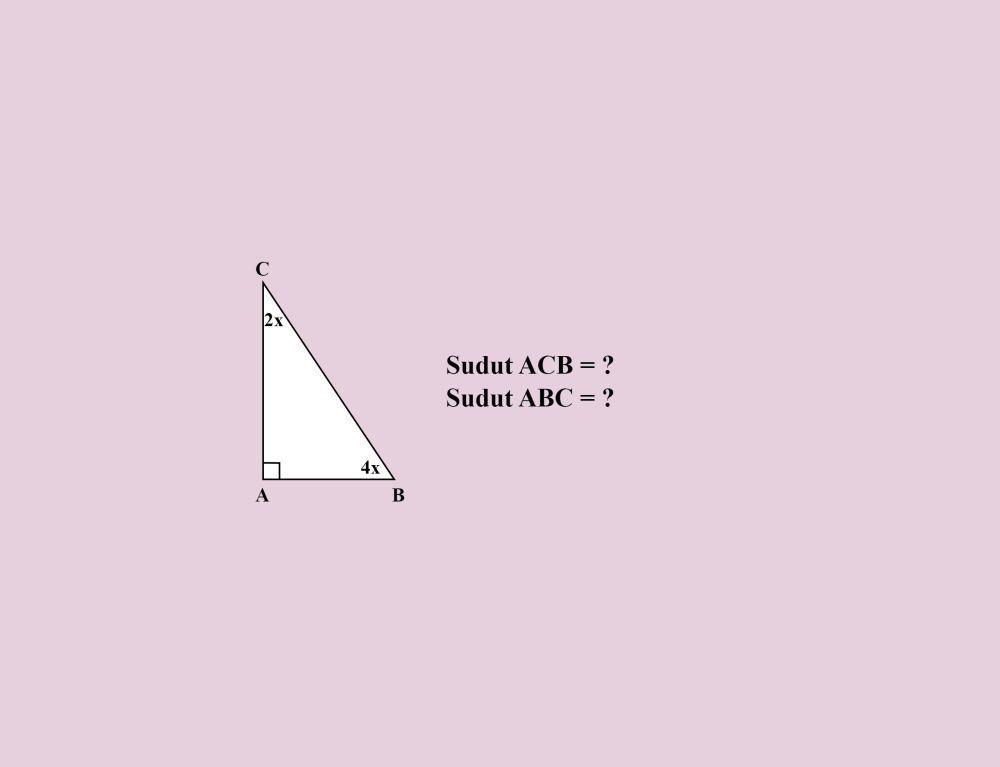
Perhatikan gambar di atas!
Berapakah besar sudut ACB dan sudut ABC?

Pembahasan:
Diketahui:
Jumlah besar sudut segitiga = 180 derajat
Sudut BAC = 90 derajat
Sudut ACB = 2x
Sudut ABC = 4x
Ditanya:
Besar sudut ACB = ?
Besar sudut ABC = ?
Jawaban:
Untuk mengetahui besar sudut ACB dan sudut ABC kita harus mencari nilai x terlebih dahulu.
Sudut BAC + sudut ACB + sudut ABC = 180
90 + 2x + 4x = 180
2x + 4x = 180 - 90
6x = 90
x = 90 : 6
x = 15

Maka besar sudut ACB = 2x = 2(15) = 30 derajat.
Sedangkan besar sudut ABC = 4x = 4(15) = 60 derajat.

Wah, kita telah selesai mempelajari rumus-rumus untuk menghitung luas dan keliling segitiga siku-siku beserta contoh penerapannya pada soal latihan. Sekarang, saatnya untuk menguji pemahaman kalian dengan mengerjakan kembali soal-soal latihan di atas secara mandiri. Semangat dan selamat belajar!